Crosswalks

Every day I save about 3 minutes by changing the series of crosswalks I take on my way to work and back. The time I spend walking is always the same, but by opportunistically choosing where and when to cross based on the lights, I save time waiting on lights to change.

Here's the chart of the expected wait time necessary to reach a destination in the northwest corner, starting from various points on the grid. I'm assuming a crosswalk alternation time of 45 seconds and that it takes 10 seconds to walk across one. Hover over points for more details.

Each square represents a city block, and each dot is one of its corners. The redness at that dot is proportional to the wait time to reach the destination from it.

If you were to go 10 blocks north, then 10 blocks west, your expected wait would be 302.6 seconds, but if you follow the ideal walking strategy starting from the same point, your wait is only 49.8 seconds! That's 84% wait time savings!

At the corner of each city block, you have up to three options:

• Go north
• Go west
• Go "diagonally"; if you are at the northwest corner, cross north and then west or west and then north. Let's zoom in closer on how likely each of those options is to be best, based on the time at which you enter the light cycle.

Your decision between these three options is determined by the (random) time into the light cycle at which you reach the intersection. This next chart shows your chance to make each decision, depending on your location, indicated by the thickness of each edge.

Again, suppose you start 10 blocks south and 10 blocks east. Let's take a look at how likely you are to pass through each intermediate block corner on your way to your destination. Here the size of each dot is proportional to your chance to reach it along the way.

Calculation

I derived this data through a breadth-first search on the expected wait time at each vertex. The exact details get nasty because of all the casework between your options each block corner, but I'll give the gist here.

Let's assume that

• Every intersections is 4-way, with 2 synchronized "north" crosswalks and 2 synchronized "west" crosswalks.
• Every crosswalk alternates between north and west every seconds (with no pause in between).
• Each day, the crosswalks are independently initialized with a uniformly random time offset between 0 and ; for instance, for , the north crosswalks are open, and for , the west ones are open.
• It takes seconds to cross any crosswalk, and you may only enter when you have enough time left to finish crossing.
• Upon reaching an intersection, you know (by scanning the time left on the active crosswalk). You can't tell for intersections you haven't reached yet.

So for instance, at a northwest block corner where all three options of crossing north, west, and diagonally are open to you, the immediate wait necessary for each option is as follows:

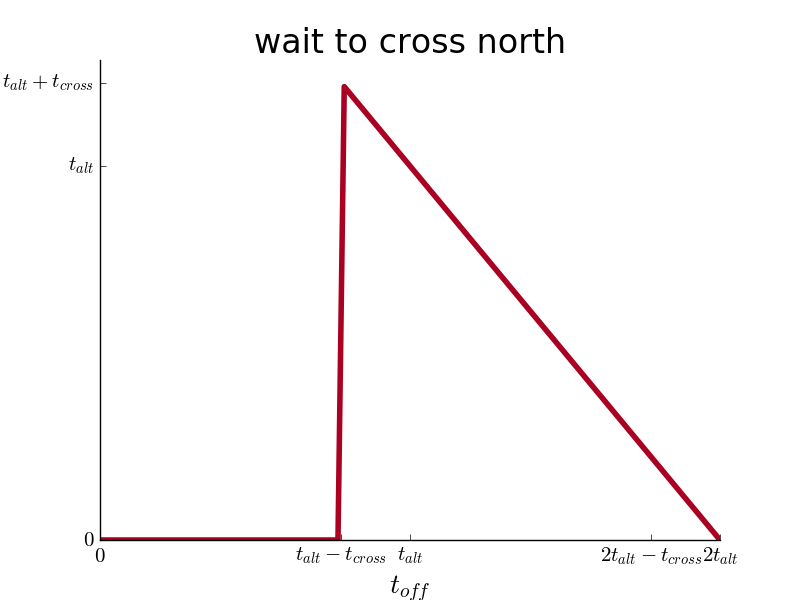
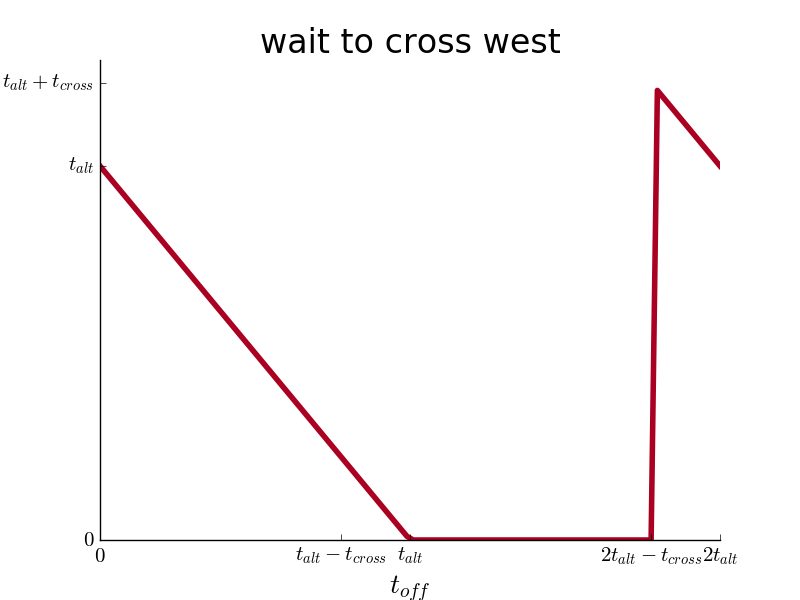
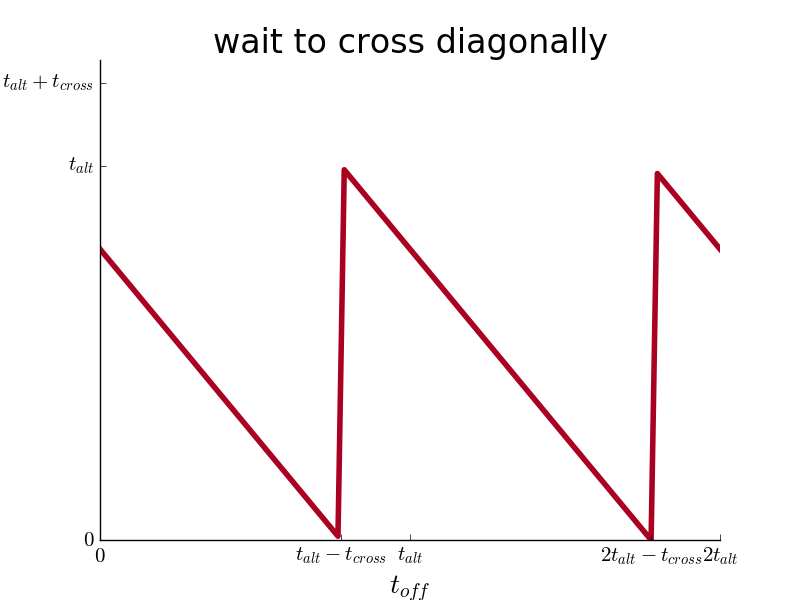
Your decision is simply guided by minimizing expected wait, so depending on , you choose the option with the minimum where is the expected wait time to cross all future intersections, following the decision. My breadth-first search calculated at each block corner, along with the nice details you saw above, like the probability to cross each direction.