Latent Dirichlet Allocation

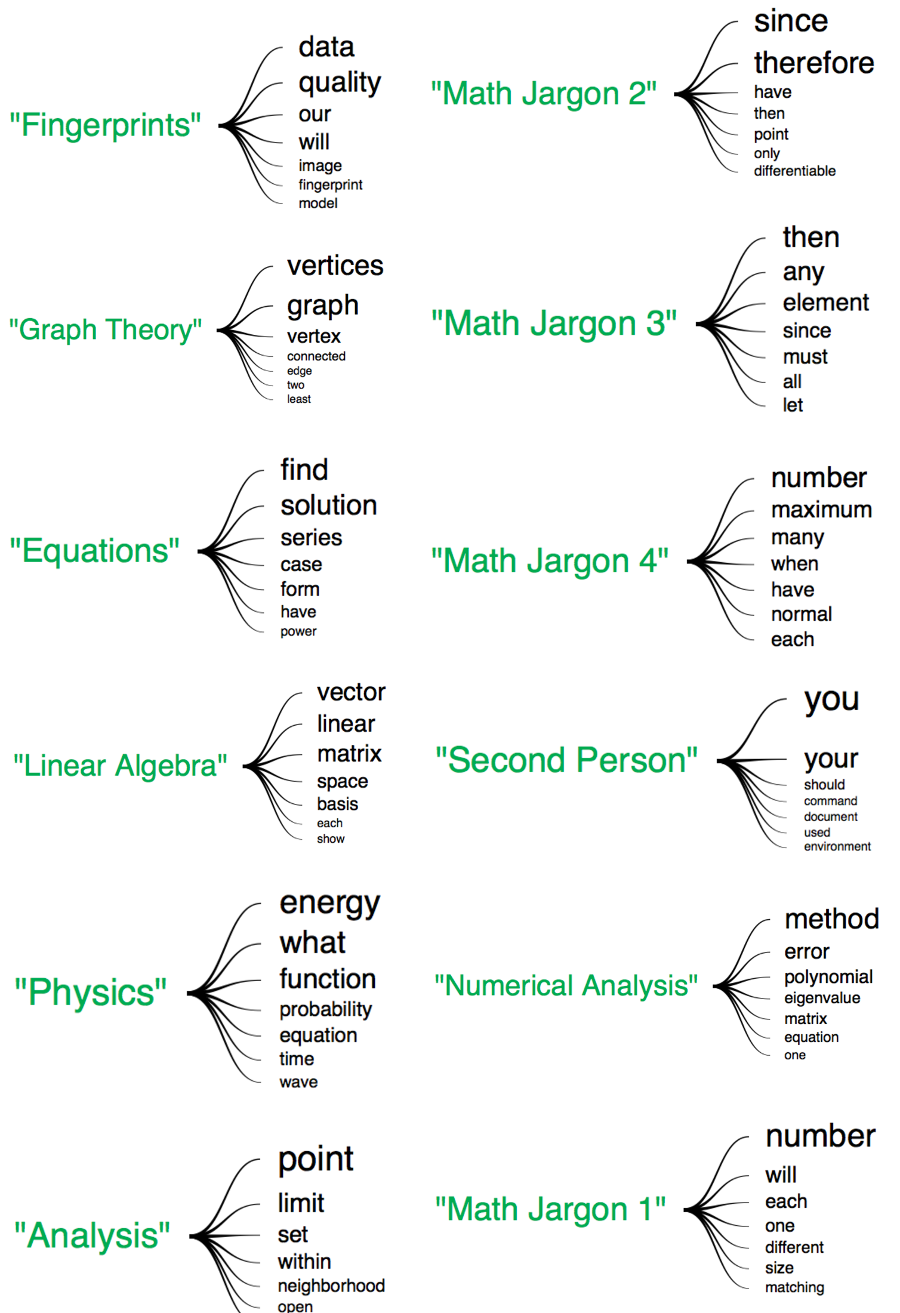
Latent Dirichlet Allocation (LDA) is a model for describing the most important topics among a set of documents. For example, Scientific American may have a topic for cosmology, characterized by increased frequency of the words "star", "space", "supernova", and such. LDA defines a topic as a list of word frequencies, and its aim is to estimate the most likely set of topics to explain the documents it sees. I implemented this model (from scratch!) and ran it on my 257 school-related .tex documents from college. This gave the following topics, characterized by their most disproportionately frequent words, which I labeled:

Latent Dirichlet Allocation There are some decent explanations of LDA here, here, and here, but the premise is this: we assume authors are senseless buffoons who chose topics and then randomly write down words from them. One of these zombies may decide to write 50% about cosmology, 30% about marine biology, and 20% about baking, which is likely to produce something like this:

Muffin dolphin trajectory space siphonophore constant fish cake curvature tensor . . .

but of course with filler words thrown in. Generating a set of documents like this would be easy if we knew the topics and the chance of each topic to occur, but our task is the inverse of this: we need to find the most reasonable set of topics, given only a set of documents and a number of topics to look for.

Calculating this set of topics exactly is nearly impossible, so instead we use Gibbs sampling - we randomly assign each word to a topic, then consider each word one by one and reassign the word according to its probability of being from each topic (which is the complicated part - this probability depends on both the word and the the topics apparently represented in its document). To prioritize important words over filler words, we use a list of the most general ones like "a" and "the" and tell LDA to ignore them. When we start Gibbs sampling, the topics will all look similar, but after enough iterations, topics will become more distinct, and words will very likely to fall into the topics they belong to.

Results

Like I mentioned before, there are only two inputs: the set of documents and the number of topics to look for (so this is an unsupervised learning algorithm). When running this model on huge sets of documents, researchers often use 100 topics, but since I was running it on just 257 documents, I looked for 12 topics. This produced the above word diagram for the top words in each category, sized according where is their frequency within the topic and is their frequency in the whole dataset. I put my code in this Github repo.

All my .tex documents come from one of three categories: math classes (primarily), team projects like my clinic project about fingerprints, or physics classes. Accordingly, we get a lot of categories of math jargon, a topic about fingerprint images and models, and a topic of physics terms. One interesting thing is the "second person" topic - I suspect it mostly comes from the comments that some of my latex documents have. I might try leaving those out next time.

And this was all done without telling the computer the nature of the topics or documents - beautiful!