Graph all the things

analyzing all the things you forgot to wonder about

Interpolation on a Sphere

2015-03-22
interests: math, geometry

We can interpolate between points on a sphere, meaning that, given the value of a function (such as temperature) at various points on a sphere (such as Earth), we can estimate the temperature between those points. For instance, here is an interpolation based on the temperatures in Bangalore, Beijing, and Moscow today, where orange is warm and blue is cold:

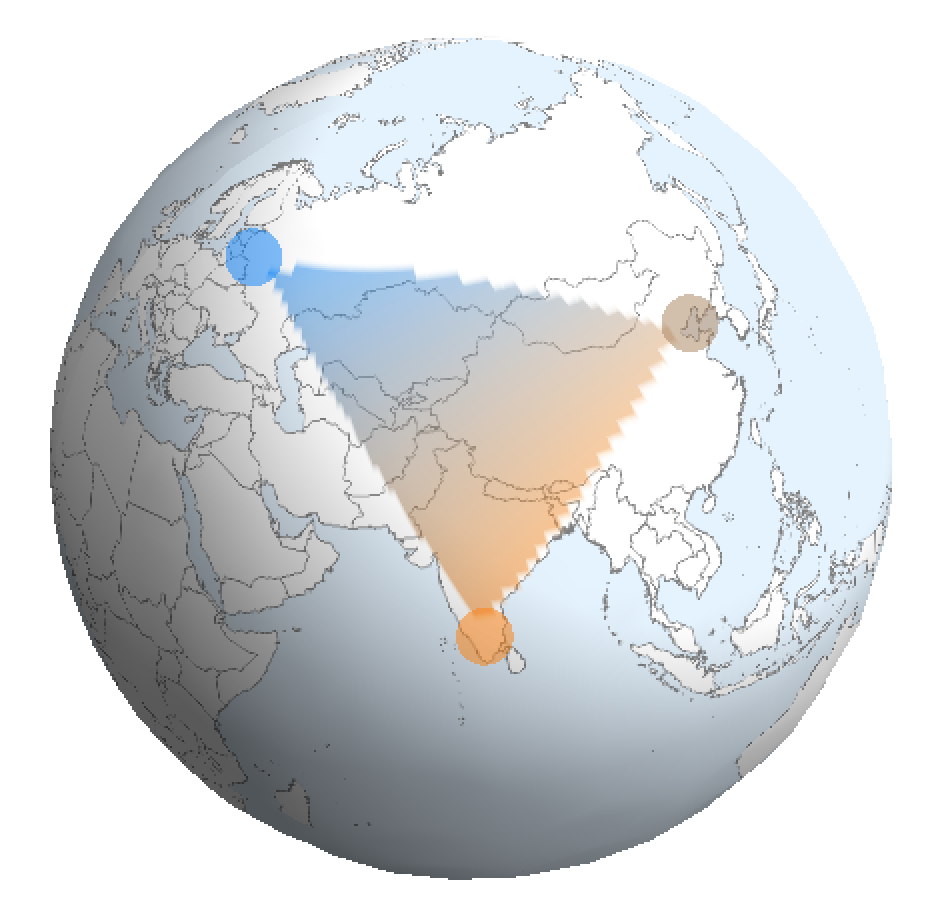
colored spherical triangle between Bangalore, Beijing, and Moscow

From geometry, we can derive an elegant method to do this to a region on a sphere. Using graph theory and enough points, we can extend this to the whole sphere (in the next post).

The Idea

Here's the temperature today in a few cities:

City	Temperature (Celcius)
Bangalore	23
Beijing	11
Moscow	-12

You want to estimate the temperature in Islamabad using this information - you're a bit crazy like that. You probably already know how to do linear interpolation on the temperature between two points on a one-dimensional line: if you know $T(x_0)$ and $T(x_1)$ , then you can estimate $T(x)$ for $x_0 \le x \le x_1$ by

$T(x) \approx \frac{x-x_0}{x_1-x_0}T(x_1) + \frac{x_1-x}{x_1-x_0}T(x_0)$

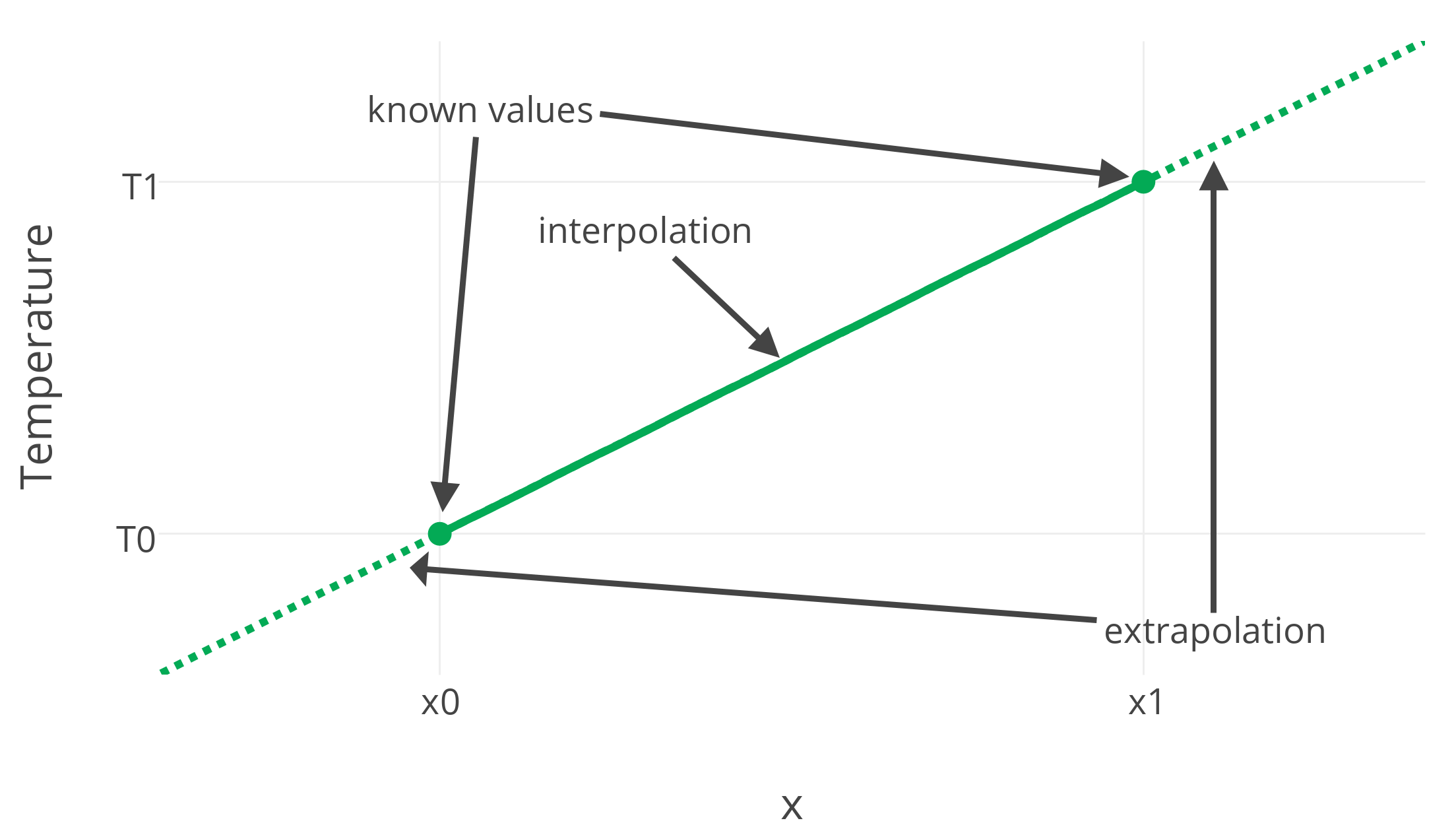
a straight line between two points; interpolation is the part of the line between the points, and extrapolation is the part beyond them

But how would you interpolate the temperature between these cities? On a surface like the Earth, the answer isn't so obvious. Not only are we working in two dimensions (latitude and longitude), but the Earth is also curved. I'll show a beautiful way to perform a "linear" interpolation on a sphere.

Planar Geometry

We can generalize our result on the line to two dimensions. Let's say you know the temperature at points $x, y, z$ and want to estimate it at $w$ within triangle $\Delta xyz$ :

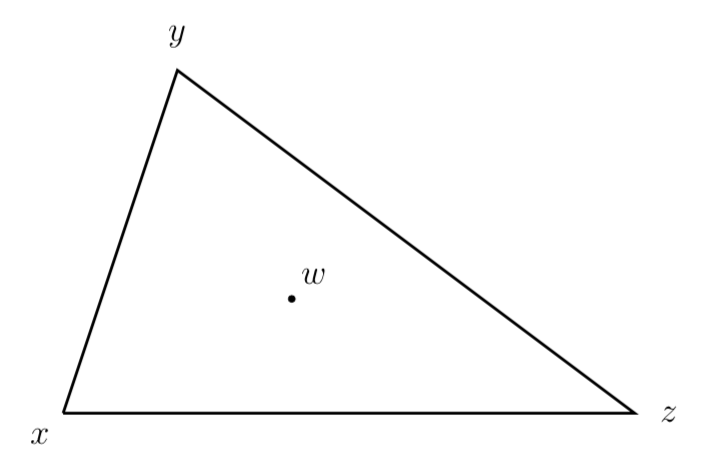
a triangle with vertices x, y, z, and a point w in the middle

We want to estimate the temperature at $w$ by $T(w) = c_xT(x) + c_yT(y)+c_zT(z)$ for some coefficient $c_x, c_y,c_z$ with $c_x+c_y+c_z = 1$ ; some mixture of the temperatures. It actually easiest to think of this in vector form, shifting the origin to be where $x$ is:

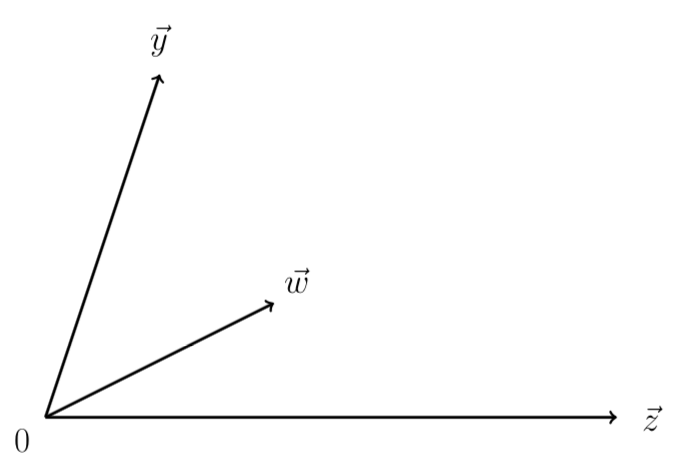
vectors from the origin (formerly x) pointing to x, y, and w

Intuitively, the coefficients for our mixture of temperatures should satisfy $c_y\vec{y} + c_z\vec{z} = \vec{w}$ , leaving $c_x = 1-c_y-c_z$ . This seems simple enough, but there is a more convenient way to write this in terms of the areas of triangles in the following figure:

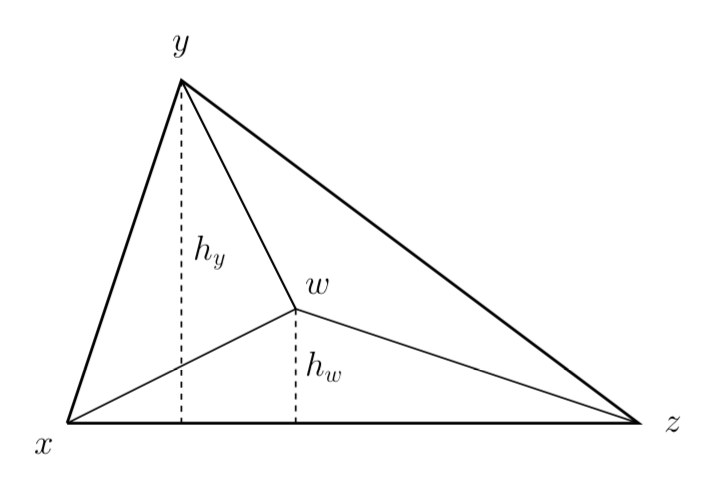
triangle with verticals drawn from y and w down to xz

Using our vectors from before, the area of $\Delta xzw$ is

$A_{xwz} = \frac12 ||\vec{z}|| h_w$

$A_{xwz} = \frac12 ||\vec{z}|| h_y \frac{h_w}{h_y}$

$A_{xwz} = A_{xyz} \frac{h_w}{h_y}$

Because of the way I have oriented the triangle, it is easy to see that $w$ 's vertical component $h_w$ is just $c_yh_y$ (since $\vec{w} = c_y\vec{y} + c_z\vec{z}$ and $\vec{z}$ is entirely horizontal). This gives

$A_{xwz} = c_yA_{xyz}$

By shifting the origin and rotating the triangle, we can apply the same reasoning to obtain

$A_{zwy} = c_xA_{xyz}$

$A_{ywx} = c_zA_{xyz}$

That is, the area of the subtriangle opposite point $p$ is proportional to the coefficent $c_p$ by a ratio equal to the the area of the whole triangle $\Delta xyz$ .

Spherical Geometry

We can actually reduce the problem of interpolating on a sphere to the problem of interpolating on a plane. This is tricky, since there is no such things as a linear function on a sphere - we can only hope for a function which is locally linear. Our previous argument using vectors also breaks down, since following vectors on a sphere in a different order gives a different endpoint. It turns out the best solution is to project everything onto a plane perpendicular to the vector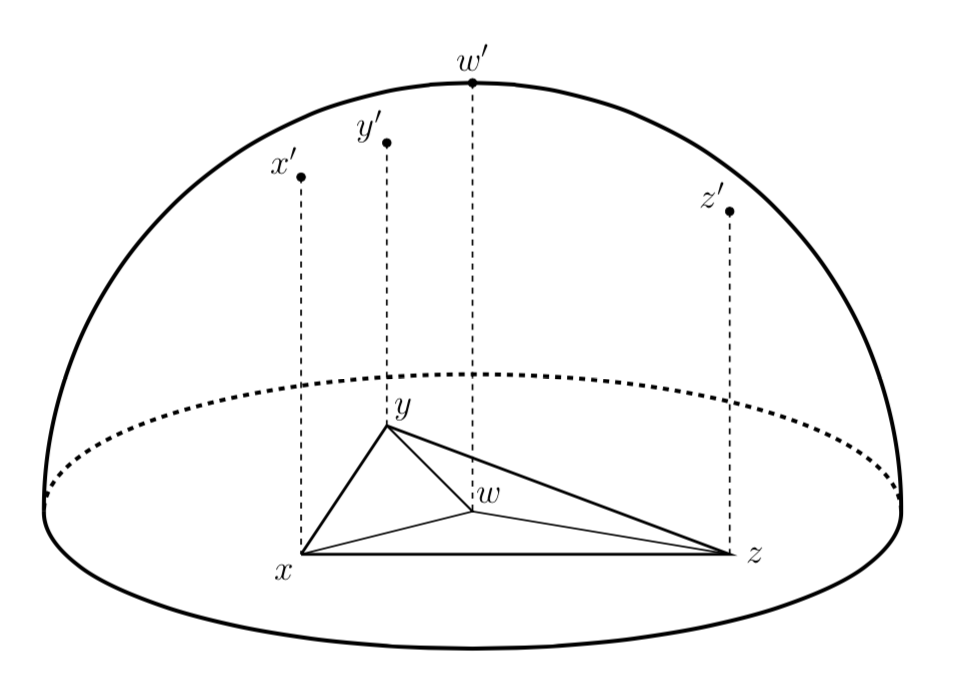 $\vec{w'}$ (drawn from the sphere's center) we want to interpolate at:

Gorgeous diagram of a hemisphere with points x', y', z', w' projected down to the flat plane of the hemisphere. Really my finest work.

Here we have positioned the plane at the base of the hemisphere so that the projected point $w$ is the center of the sphere and the origin. At this juncture, one might despair because actually calculating the projection and evaluating areas from it would be tedious. But fear not: there will be a deus ex machina, and that machina is the determinant. If we take three vectors such as $\vec{x'},\vec{w'},\vec{z'}$ (in 3-space, drawn from $w$ ) and stuff them into a matrix (as its columns), the determinant $\det(\vec{x'},\vec{w'},\vec{z'})$ of that matrix is very special. Its magnitude is $3V_{wx'w'z'}$ where $V_{wx'w'z'}$ is the volume of the tetrahedron formed by $w,x',w',$ and $z'$ . Its sign indicates whether $x',w',z'$ are in counterclockwise order or not, which is a useful fact I will get to in my next blog post.

Anyway, the volume of a tetrahedron is actually extremely useful. You may recall from geometry class that $V_{wx'w'z'} = \frac13 Ah$ where $A$ is the base's area and $h$ is the height. From its projection onto the plane, we can choose $A=A_{xwz}$ and $h = ||\vec{w'}||$ , we get

$|\det(\vec{x'},\vec{w'},\vec{z'})| = A_{xwz}||\vec{w'}||$

$|\det(\vec{x'},\vec{w'},\vec{z'})| = c_yA_{xyz}||\vec{w'}||$

And by the same reasoning,

$|\det(\vec{y'},\vec{w'},\vec{x'})| = c_xA_{xyz}||\vec{w'}||$

$|\det(\vec{z'},\vec{w'},\vec{y'})| = c_zA_{xyz}||\vec{w'}||$

In other words, the determinant of the matrix formed by the desired point and two of the known points is proportional to the coefficient for the remaining point by a fixed ratio. So determining the relative proportions of these determinants gives the desired coefficients $c_x, c_y, c_z$ - a very simple task.

Result

Using this calculation, we estimate that the temperature in Islamabad is a mixture of 51% that of Bangalore, 14% that of Beijing, and 35% that of Moscow, for a result of 9 $^\circ$ C. We can also plot the result of this interpolation:

The actual temperature there is 15 $^\circ$ C, which is pretty close (lucky) considering that temperature can vary unpredictably across just a few hundred kilometers. To accurately estimate the temperature using this method, we would need to measure it it many more points; apparently NOAA uses something like 1500 weather stations around the globe. By the time I finished writing this, temperatures had changed slightly, but here's a real heat map of Asia:

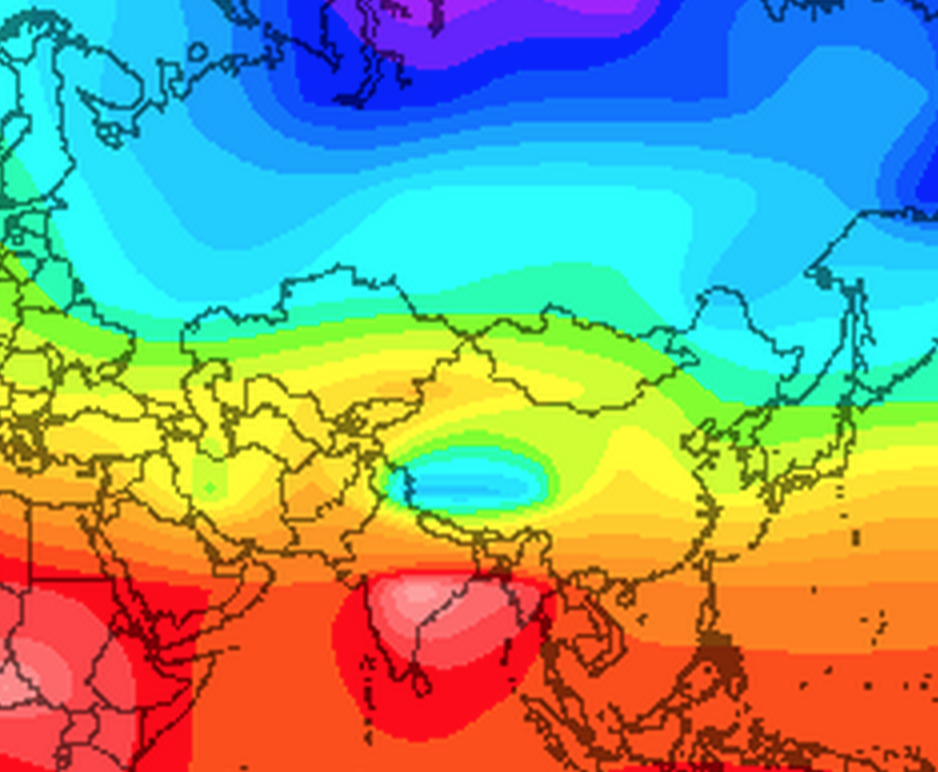
actual heat map of Asia from weather site

I'll show one way to interpolate with very many known points in my next post.

< previous next >