
Graph all the things
analyzing all the things you forgot to wonder about
Map Projections 5: More Interruptions
2024-04-13
interests: maps
In parts 1, 2, 3, and 4, I explained why and how I'm training optimal map projections and showed a variety of maps I trained.
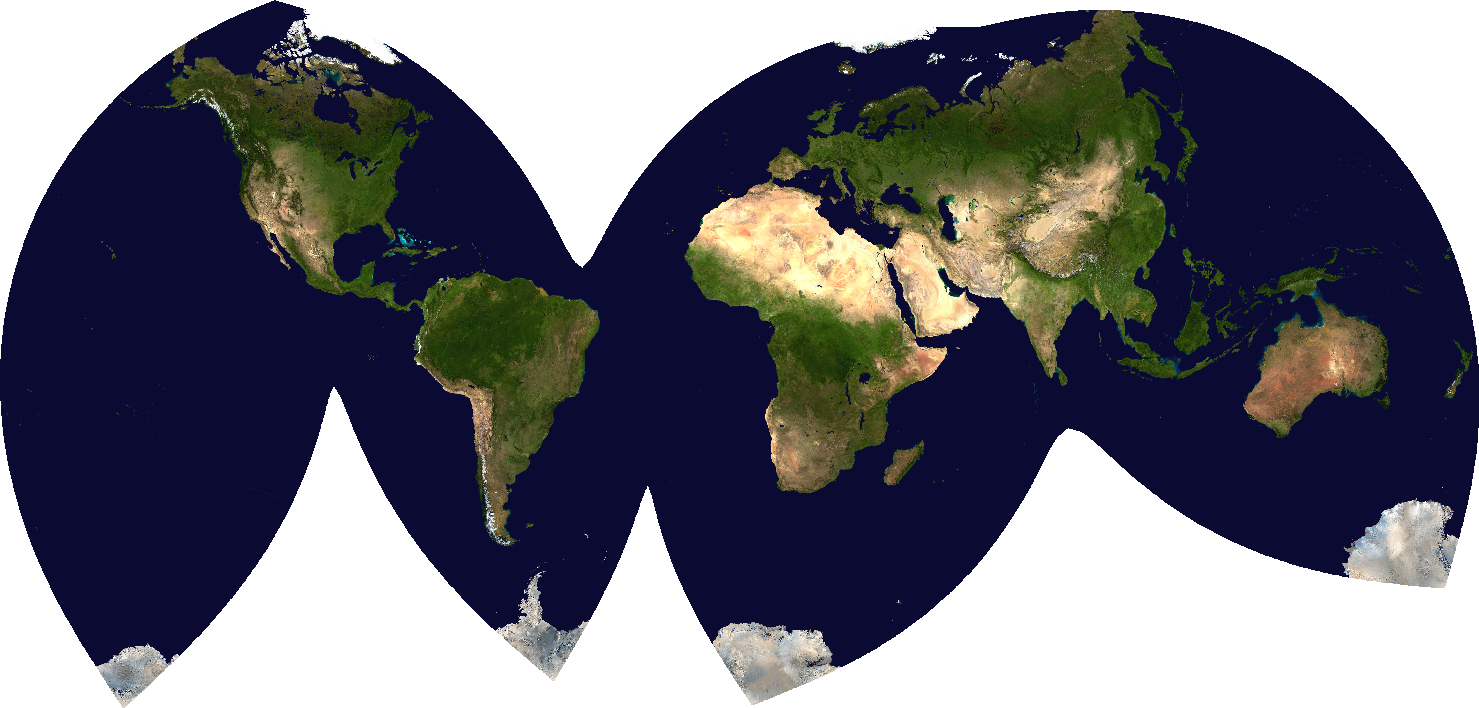
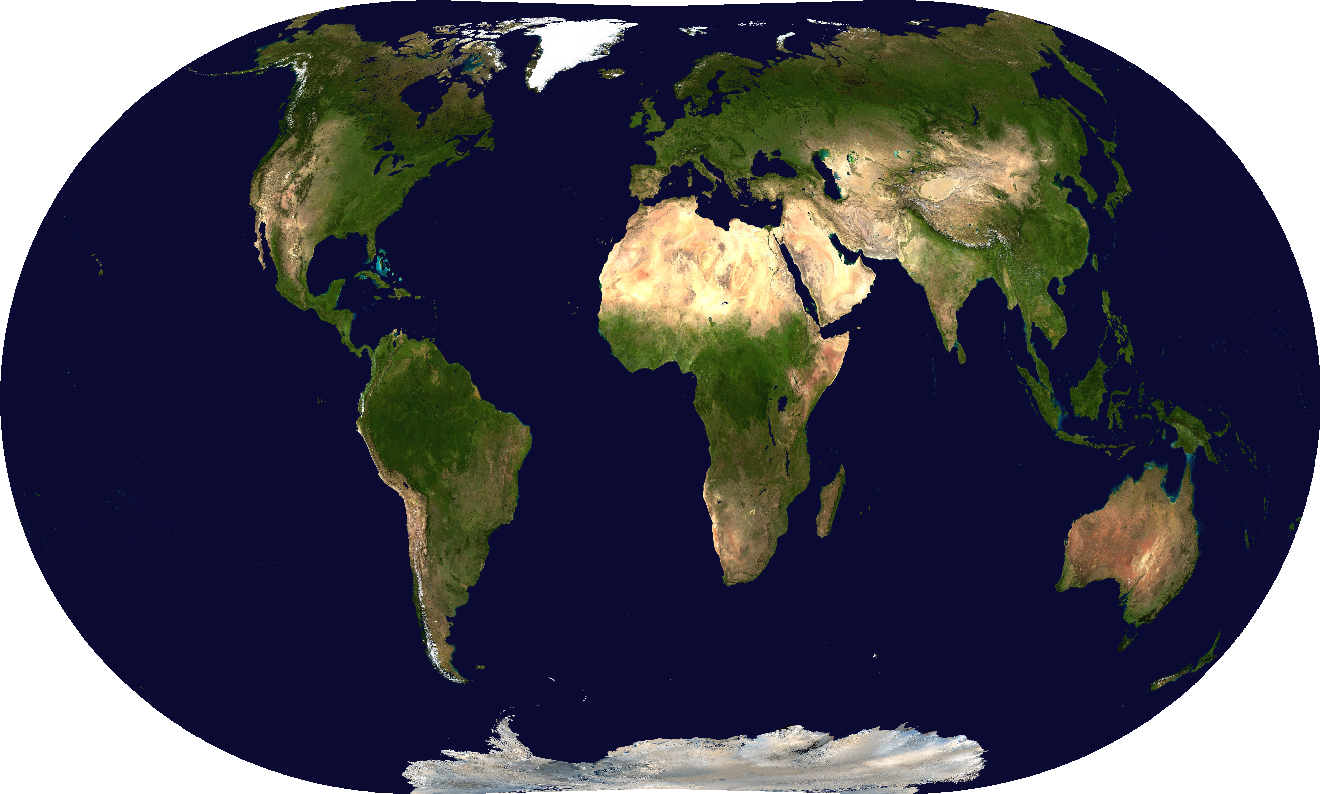
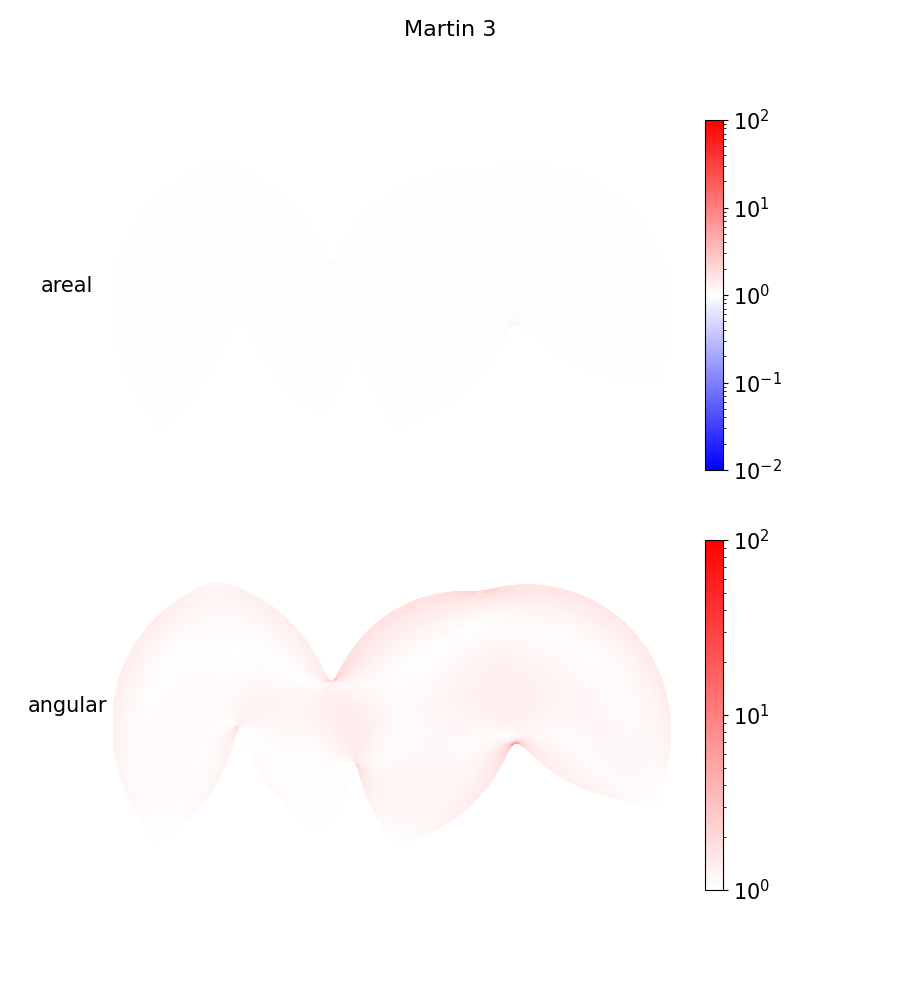
Now I've trained map projections with more interruptions. I'll call this basically-equal-area one Martin 3:
Interruptions re-explained
(See part 2 for a bit more about this.)
Imagine you're adrift in the Pacific ocean and swim west from longitude in the western hemisphere.
After a few short kilometers, you'd reach
in the eastern hemisphere.
Obviously you swam a modest distance, and you'll have to try a lot harder than that to cross the Pacific.
But on our most common map projections, that short swim takes you all the way from the left side to the right side.
That's because these map projections "interrupt" along the anti-meridian at
longitude, slicing the globe so that it can be flattened.
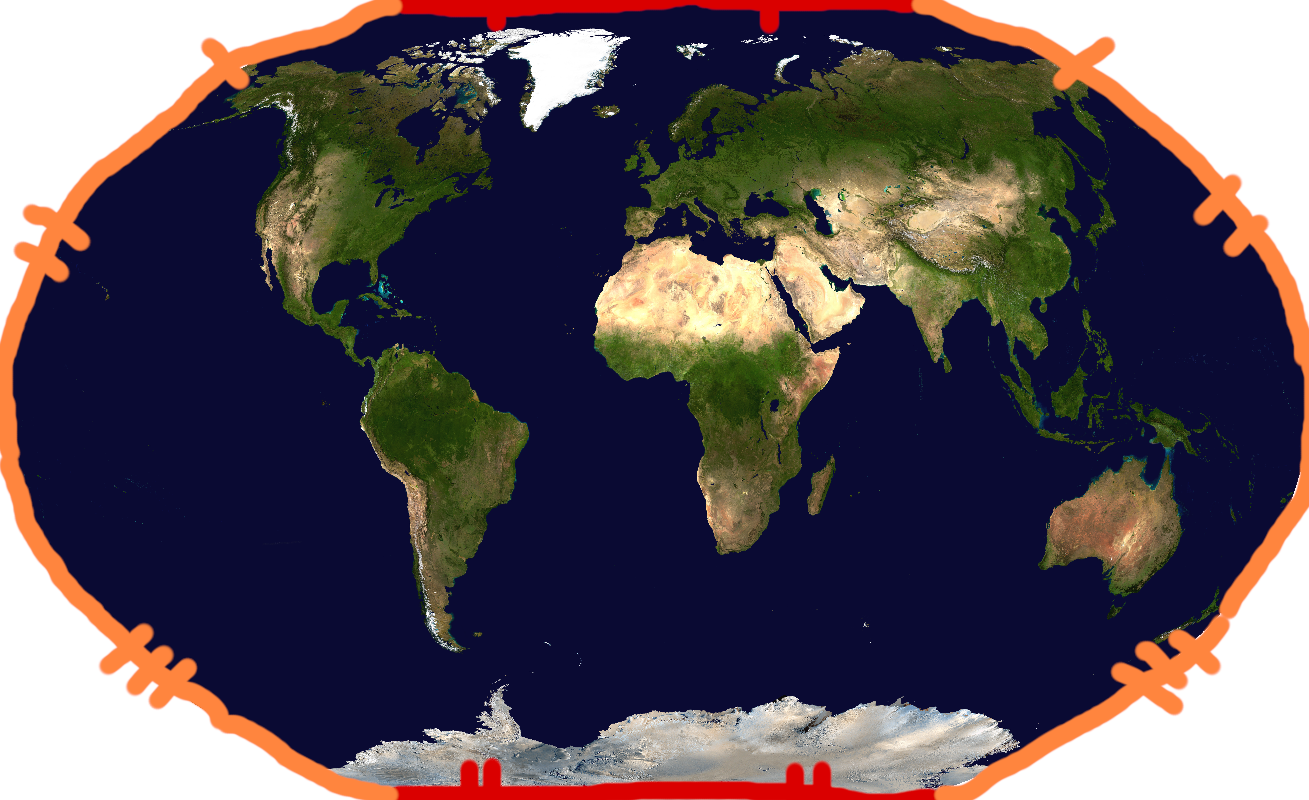
Interrupted points on the globe appear at least 2 times in the map projection. Let's take Mollweide and Winkel Tripel projections as examples. Mollweide has 2 copies of each point on the antimeridian, except for only 1 copy of the north and south poles. Winkel Tripel has 2 copies of each point on the antimeridian, except for infinitely many copies of the north and south poles.
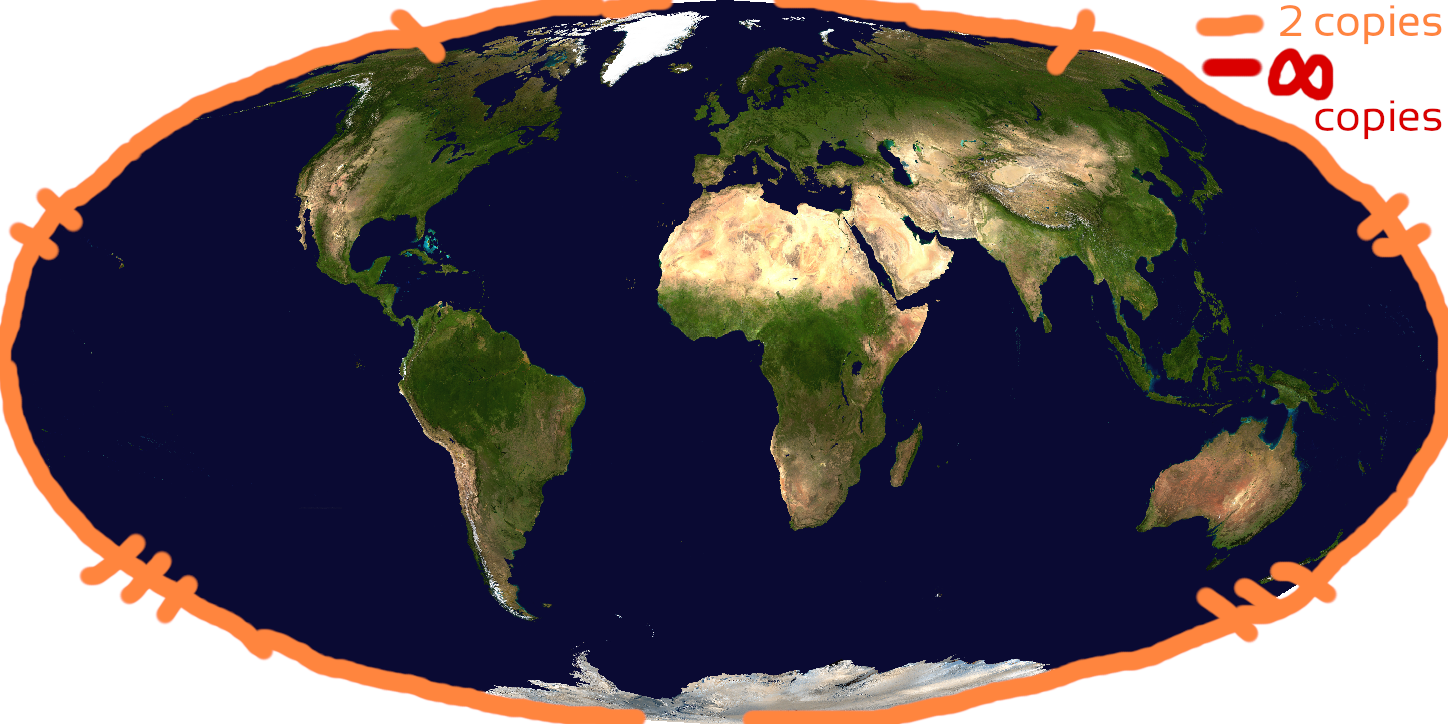
Winkel Tripel
It is impossible to project the whole globe without interrupting at at least one point. We could try to squeak by with the minimum, as azimuthal map projections like this one do:
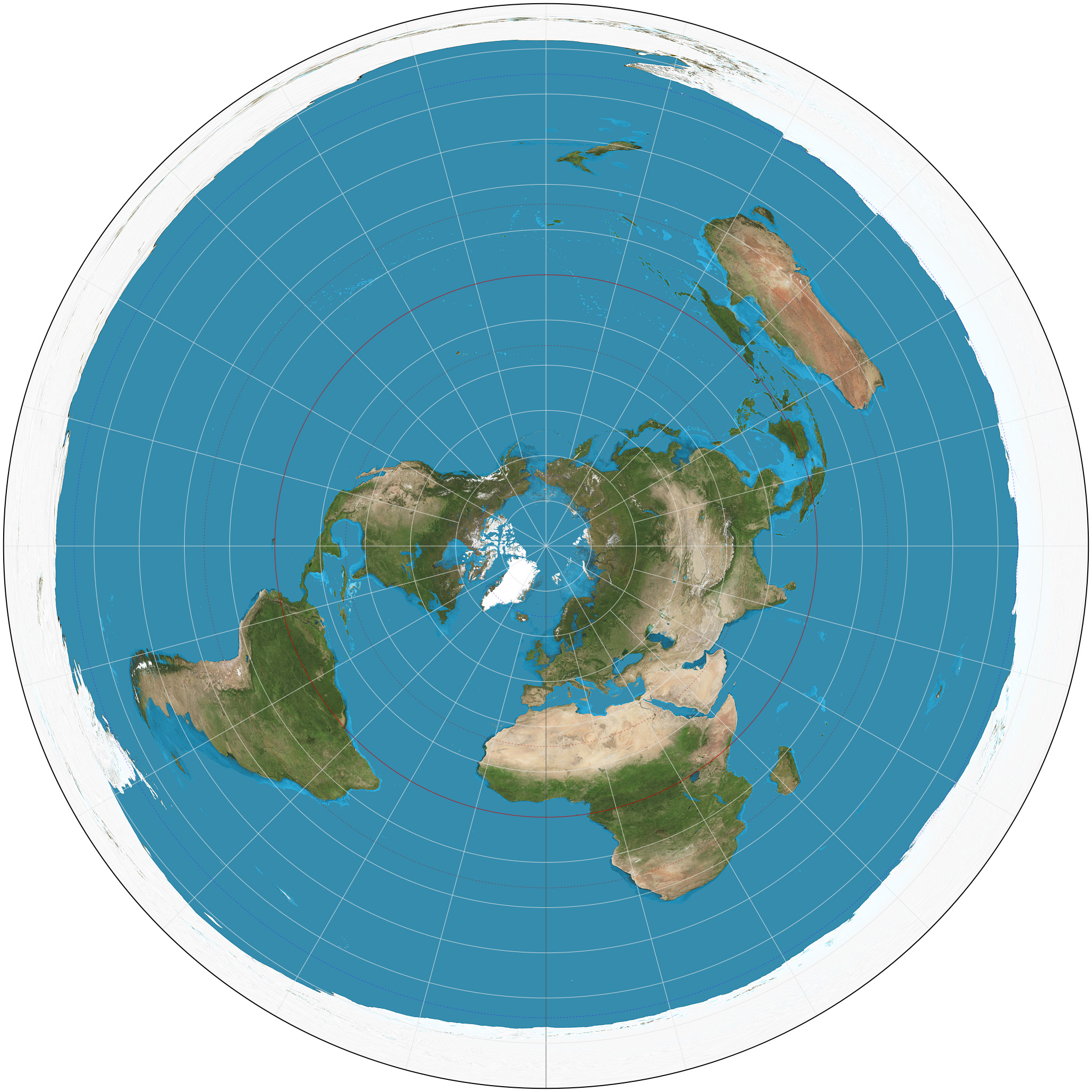
But that leads to horribly distorted maps. So in this part, I'm going in the opposite direction, interrupting along more lines to reduce distortions.
vs. Goode homolosine
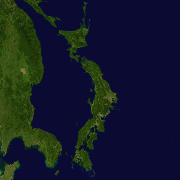
Goode homolosine is probably the most famous extra-interrupted projection:
It's equal-area and has a piecewise definition, switching from Sinusoidal to Mollweide at latitude (Why this number? No idea).
The piecewise definition makes it look like a real Frankenstein's monster.
Look at this nonsense!

Goode homolosine has 5 interruptions:
(pole to pole),
in the northern hemisphere (equator to pole) and
,
, and
in the southern hemisphere (equator to pole).
Curiously, the extra interruptions are entirely optional, and formal descriptions of the projection only mention them as a special bonus. But this is the format you'll usually see.
Martin 3 is also practically equal-area, but with slightly less interruption.
In Martin 3, the northern hemisphere interruption starts at , and the southern hemisphere ones start at
, except for the middle
one, which starts at
.
I chose these starting points for the interruptions mostly by trial and error, looking for good balance and aesthetics.
Using the exact same interruptions as Goode homolosine caused the trained projection to overlap with itself in places, which was clealy unacceptable.
Rather than programming complicated constraints, I simply zipped up the interruptions a bit so that the optimal solution no longer required overlap.
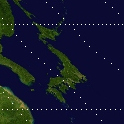
Martin 3 also has less angular distortion than Goode homolosine. Just look at how much better it treats Japan!
vs. less interrupted optimal maps
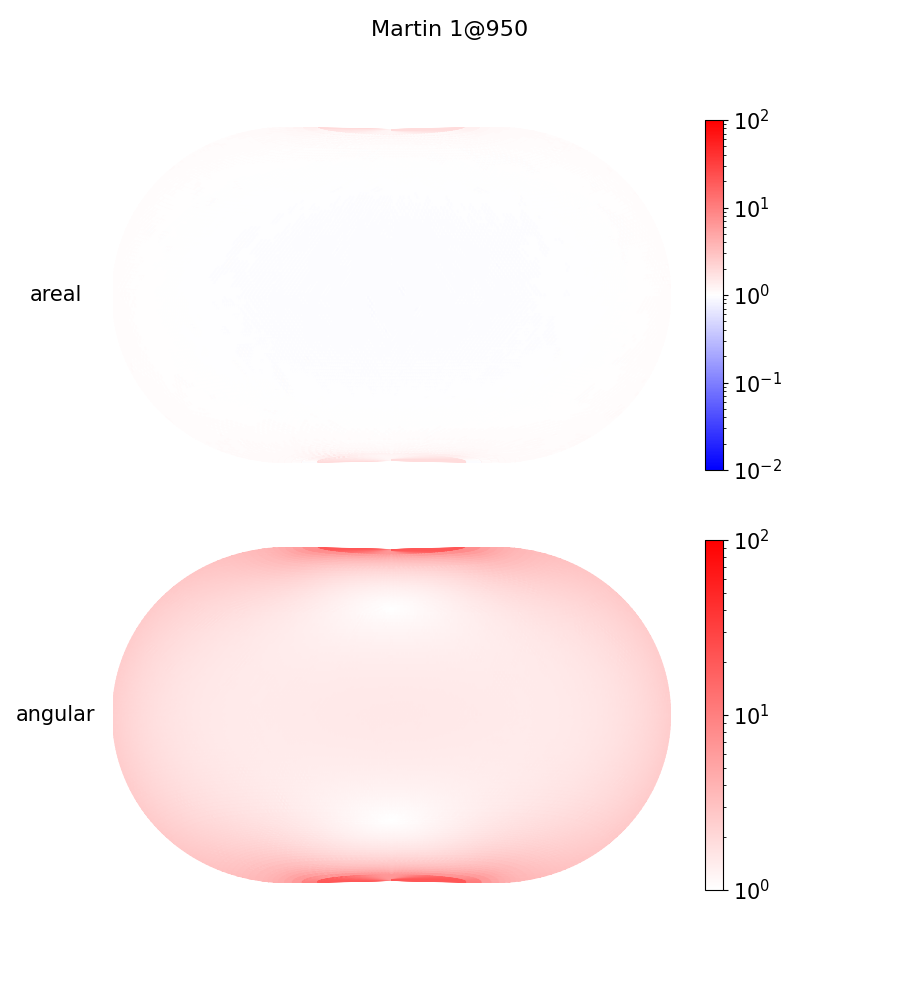
Let's compare Martin 3 versus a less interrupted optimal projection trained in the same way (which I'll call Martin 1@950):
Martin 3

Obviously interruptions are undesirable, but I might argue that Martin 3 is actually prettier. The landmass shapes just look much better! By adding interruptions, we loosened our constraints, allowing us the optimizer to greatly reduce distortion around the globe:
That's it for the map projection series! For now, at least.
One more interruption
For the past 111 months I've poured energy into this blog for two reasons: to sate my own curiosities and share interesting results with friends, acquaintances, and curious internet strangers. The median post took me about 20 hours, and some took much more. This is the 35th post, and I've also hit 10 dead ends and built one secret simulator game I spent 200 hours on before deciding it wasn't fun. I even did frontend engineering fulltime for several months in 2016 to learn D3 and React, largely for this blog. It's been rewarding, and I couldn't ask for more. But I'm going to take focus off the blog for now.
My reasons are similar to those of Every Frame a Painting (one of my favorite Youtube channels, 2014-2016): I'd like to focus on other things, and it feels like time.
Until recently, I always had more interesting ideas than time to explore them. I think that could have continued forever, but lately I've moved my sights from "finding curiosities" to "solving problems". Pcodec is part of that. This map projection series was the last curiosity on my backlog. So in the words of Bill Watterson,
"By the end of ten years, I'd said pretty much everything I had come there to say. It's always better to leave the party early."
The body of work and play that is graphallthethings.com will remain online, so don't worry. And I might still make an occasional lower-effort post. On the bright side: I may now have a bit more time to spend with those friends, acquaintances, and curious internet strangers.