Reinforcement Learning

I made an AI to play a simple game by using reinforcement learning via a value function on game states. Motivation:

• Training muscle-based creatures to walk
• Learning a good vertical-axis wind turbine shape

Basically, I wanted my own amusing progression story. The game I designed is really minimalistic: you play as a circle on a 2D square and move with fixed speed , trying to collect as many "coins" as possible. At fixed intervals a new coin will spawn on a random point on the square. Here's the AI learning.

Trained on 0 games, earning 21 points:

Trained on 9 games, earning 36 points:

Trained on 50 games, earning 57 points:

Trained on 250 games, earning 73 points:

The AI model

The AI takes in the following 3 pieces of data when choosing a target coin to move toward:

• , the normalized time. The game ends when reaches 1
• , the player's position in 2D coordinates
• , the matrix of coin positions

Value reinforcement learning works by equipping the AI with a function , meant to predict the expected number of points it has yet to gain in the game state. If this function is accurate, it should be easy for the AI to decide which move to take next. If it targets the th coin available, the next game state (ignoring new coins) will have expected points, where is the matrix without the th coin. The AI should simply target the coin which maximizes this function.

I created a natural model for using tensorflow:

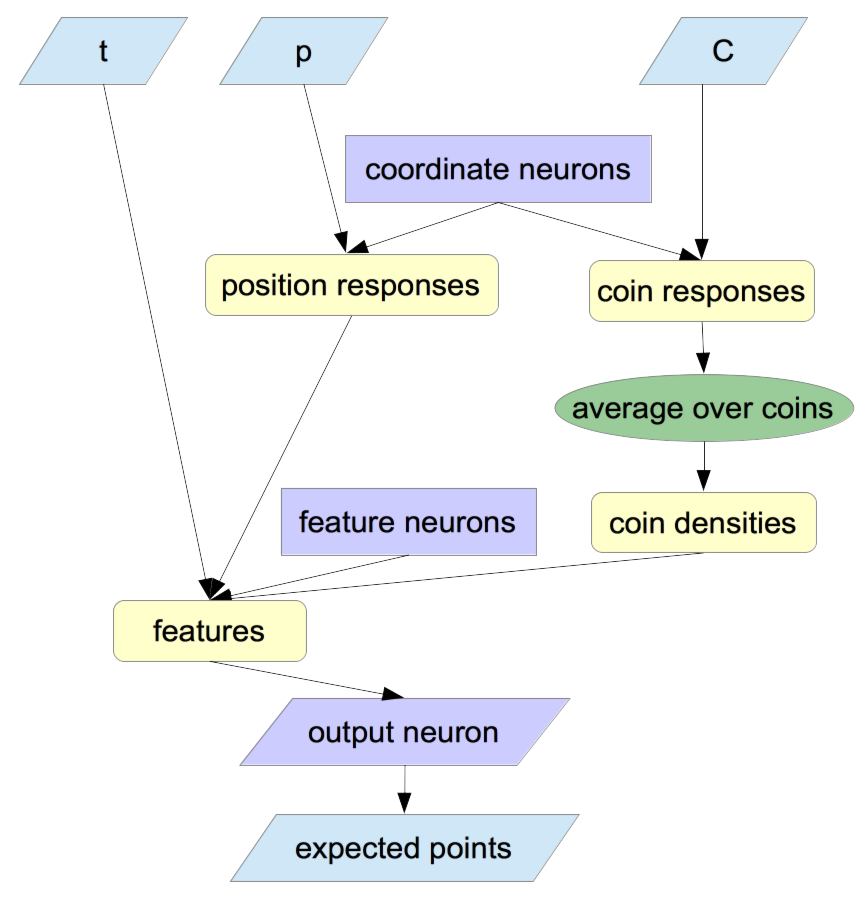
All positions (for coins or the player) are interpreted by the "coordinate neurons". Those normalized responses, as well as , are fed into feature computation. Those features are weighted by the single output neuron. The output neuron is linear, while all others use tanh.

To train the network, I took 100 snapshots of the game state as it progressed, as well as the final score. From that data, I could calculate the gradient of the loss function (just , where is final score and is the score during the snapshot) and update coefficients for all neurons.

Knowing this, the progression above should have new meaning: from 0 to 50 iterations, the AI was mostly learning not to play favorites with different parts of the board, and after that it was learning some of the finer details about tradeoffs between saving time and getting closer to clusters of coins. It still wasn't perfect at making those tradeoffs, but you can at least see that it tried.

Human Learnings

To get this AI learning consistently and quickly toward a good extremum, I made a few optimizations:

• Bootstrap the AI on another. In value reinforcement learning, there are lots of extrema where the AI will only collect lousy data because it only knows how to play in a lousy way, and these can be avoided if you train on a decent AI for a while. I ultimately bootstrapped on a greedy AI by training from games where each choice is made based on the average of the greedy AI's and training AI's objective functions.
• Add a cost term for coefficients (for tanh neurons) that get too large. In a neural network, large coefficients can make gradients shrink to 0 and learning crawl to a halt.
• After each new game, retrain on some cases from old games. This helped balance the learning algorithm's direction, and it was practical because playing games was the performance bottleneck.