Bollards

2015-01-25
interests: physics, tinkering, ODEs

A bollard is a thick metal post used at piers for mooring ships. Sailors often don't tie their ship's rope directly to the bollard - instead they wrap a rope around the bollard, then tie the rope to something else.

You may be wondering if the bollard it the most ~~boring~~ amazing thing you have ever heard of. It isn't, but if you wrap a rope around one just three times, a pencil could hold your ship in place.

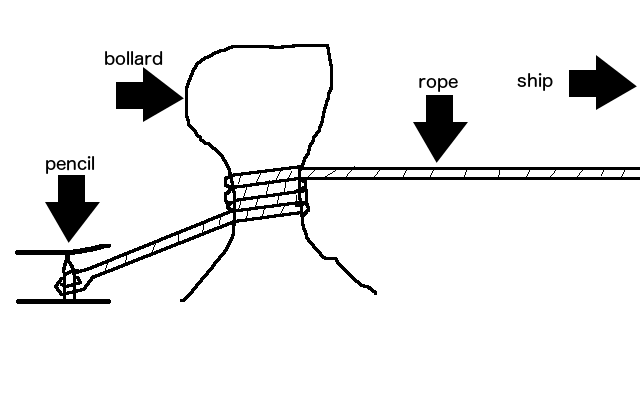
a rope wrapped around a round bollard, tied to a ship at one end and the middle of a pencil at the other

This works for the same reason why belaying a rock climber makes any sense.

The reason

If an object is pushed into a surface with force $F_N$ , the force required to make it move is

$F_f = \mu F_N$

where $\mu$ is called the static coefficient of friction (as opposed to a kinetic coefficient of friction which determines the frictional force when the object is already moving). For a rope wrapped around an object, though, things get complicated. Consider a very small section of this rope, wrapped around an angle $d\theta$ :

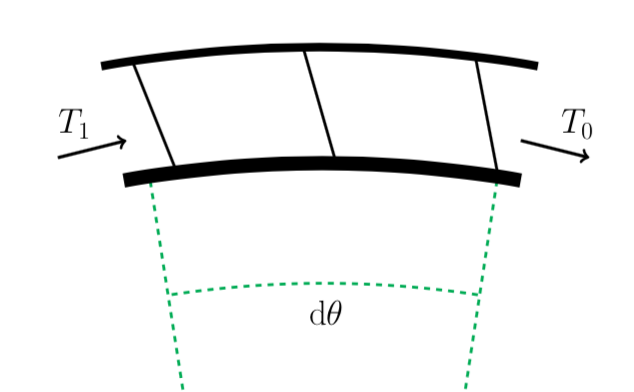
tension diagram with a rope wrapped around an angle d theta

If the tension (force pulling) on the right section of rope is $T_0$ , then the vertical component of this force is $T_0\sin(d\theta/2)$ . Since $d\theta$ is very small, the left side of the rope has a similar tension, $T_1= T_0+dT$ . That means the force of friction resisting the rope's motion is about $2\mu T_0\sin(d\theta/2)$ . It also means that $\sin(d\theta/2)\approx d\theta/2$ , so the force of friction is really just

$T_f = \mu T_0d\theta$

Thus the tension on the left section of rope is $\mu T_0d\theta$ less than on the right side. This gives us a differential equation:

$\frac{dT}{d\theta} = -\mu T$

If the rope is wrapped around any angle $\theta$ , we have that the tension at one end is

$T_1 = T_0e^{-\mu\theta}$

So the tension on the rope decreases exponentially around the bollard! A typical $\mu$ for ropes on metal is 0.4, meaning that one turn decreases the rope's tension to less than 1/12 of the ship's force. Three turns decreases the force by a factor of about 1900, meaning that a ship's 140,000-Newton force could be reduced into a 74-Newton force - not even enough to break a pencil. You can read everything else you ever wanted to know about bollards in Friction Coefficients of Synthetic Ropes.

Why rock climbing works

Usually people rock climb in pairs: a belayer and a climber. They are connected by a rope going through various metal draws. If the climber falls, the rope will grow taut on the uppermost draw as the belayer's weight stops the fall.

photo of sport climber clipping rope through a carabiner

If the rope were frictionless and the climber were heavier than the belayer, this would not happen; the climber's tender brains would continue to plummet toward the rocky floor. The only thing preventing such a tragedy is the friction between the draw and the rope: when the rope grows taut, it will be wrapped around 180 $^\circ$ of metal. Climbing ropes are relatively smooth with a kinetic coefficient of friction of $\mu_K\approx0.24$ . Nevertheless, that is still high enough to reduce the tension on the belayer's side of the rope to only half as much as the tension on the climber's side. In principle, someone half your weight could belay you (though your fall might be quite long before it ends), and this is all due to the exponential way that tension decreases along a rope that is wrapped. I thought that was cute.

< previous next >